Fonctions polynômes de degré 2

$f$ est une fonction polynôme de degré 2 si,et seulement si, on peut l'écrire sous la forme $ax^2+bx+c$ avec a,b,c réel et a≠0.

Les nombres a, b, c sont les coefficients du polynôme.

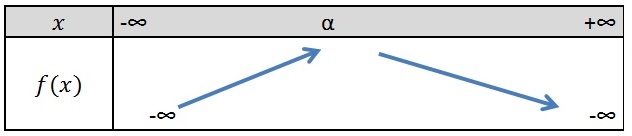
Le signe de a détermine le sens de variation de la fonction polynôme.

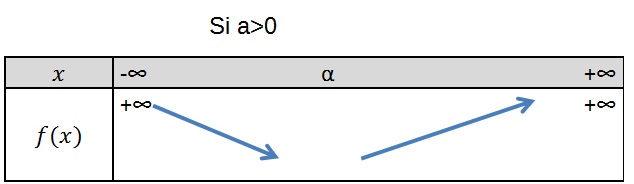
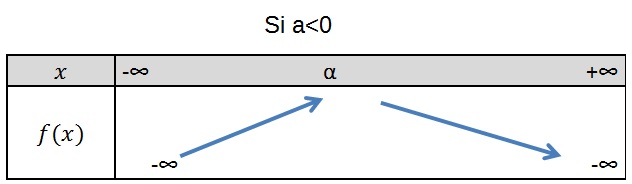
On note que la parabole possède un axe vertical de symétrie en $x=α$ (voir comment trouver cette valeur dans l'exemple).

Exemple : Trouver les coefficients du polynôme $-(5x+2)^2+20$. Faire son tableau de variation.

Réponse : On développe l'identité remarquable. Attention, celle-ci est précédée d'un signe moins. On doit donc laisser le résultat de l'identité remarquable entre parenthèses.

$\table -(5x+2)^2+20,=,-(25x^2+20x+4)+20;,=,-25x^2-20x+16$.

Les coefficients sont donc -25;-20 et 16. le coefficient de $x^2$ est négatif, le tableau de variation est donc de la forme:

On peut trouver α: comme $(5x+2)$ est au carré, il est positif ou nul. On trouve que $5x+2=0$ pour $x=-2/5=-0.4$. A ce moment $-(5x+2)^2+20$ est maximum. Donc α=-0,4. On peut donc trouver les coordonnées de ce point, il nous faut trouver son ordonnée. On calcule $f(0,4)=-(5×0,4+2)^2+20=20. Le sommet de la parabole est en (-0,4;20). Ce point est le plus important pour tracer la courbe représentative puisque c'est l'endroit où la fonction change de sens.